具有低功耗低成本性能的 PCB 罗氏线圈与积分电路设计

[ABC]

本文转自TI的应用笔记文档（ZHCA710 – Jun. 2017）
作者：Wiky Liao / Kevin Zhang
PDF文档下载链接：https://www.123865.com/s/2Y9Djv-1uTdH

摘要

PCB 罗氏线圈以其响应速度快、线性度优良、成本低等特点，在交变大电流场合中得到了广泛应用，如交流电机控制、扶梯、架空线和电缆等。由于罗氏线圈的输出信号是原始电流的微分，因此需要搭配设计积分电路。本文详细介绍了 PCB 罗氏线圈的工作原理及设计要点，并以 TI 运放 OPA2333 设计出高性能积分电路，可帮助客户快速设计出符合应用需求的 PCB 罗氏线圈电流检测方案。

1 罗氏线圈

1.1 罗氏线圈简介

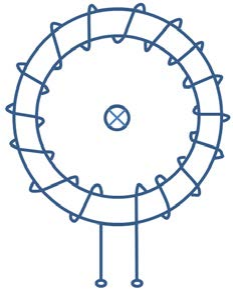
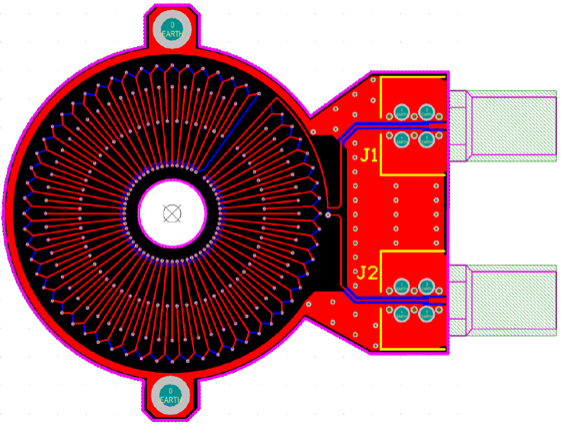
罗氏线圈是一种非接触式电流传感器，主要分柔性和硬性两大类，PCB 罗氏线圈便属于硬性罗氏线圈。其结构特点为导线均匀绕在非磁性环形骨架上，形成一个环形线圈，被测电流从线圈中心穿过，如 Figure 1 所示。

Figure 1 左图为罗氏线圈结构简图，右图为 PCB 罗氏线圈 Layout

1.2 罗氏线圈工作原理

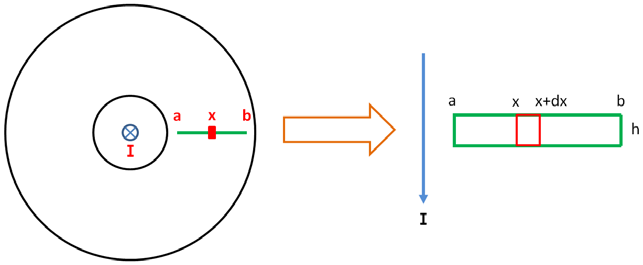
假设一根无限长载流导线垂直穿过罗氏线圈中心，导线电流为 I。线圈内径为 a，外径为 b，板厚为 h，PCB 导线的磁导率为 μ。如 Figure 2 所示。

Figure 2 罗氏线圈分析模型，左图为俯视图，右图为剖视图

根据 Biot-Savart 定律，x处的磁感应强度：

B = \mu \frac{I}{2\pi x} \tag{1}

顶层导线与底层导线通过过孔相连，组成 1 匝，每匝产生的磁通量：

\phi = \int_{a}^{b} B \times dS = \int_{a}^{b} B \times (dx \times h) = \frac{\mu \times I \times h}{2\pi} \times \ln \frac{b}{a} \tag{2}

根据楞次定律，N 匝线圈感应出的电压：

V = N \frac{d\phi}{dt} = N \times \frac{\mu \times h}{2\pi} \times \ln \frac{b}{a} \times \frac{dI}{dt} = M \frac{dI}{dt} \tag{3}

式(3)中，M 为互感系数。

由式(3)可知，罗氏线圈的输出是一个电压，它与测量的电流呈微分关系，故罗氏线圈仅适用于交流电流测量场合，并且使用中需要搭配积分器。

1.3 PCB 罗氏线圈设计要点

1.3.1 匝数限制

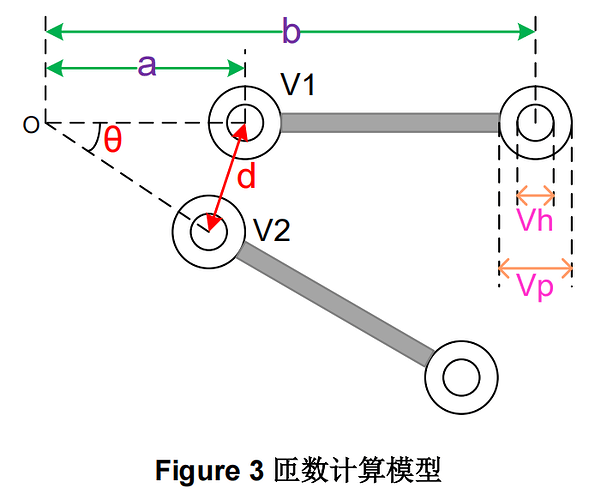
罗氏线圈的主要参数是互感系数 M，它的值主要与匝数、板子厚度、线圈内径和外径有关。其中，受限于 PCB 过孔大小和制造水平，实际上的匝数不可能无穷大，有一定的限制。匝数计算模型如 Figure 3 所示。

过孔 V1 和 V2 间的距离：

d = a \times \sin\theta \tag{4}

受限于制造水平，这两个相邻过孔间的距离至少应大于 3 倍焊盘与过孔的直径差，即：

d \geq 3 \times (V_p - V_h) \tag{5}

其中 V_p 是过孔的焊盘直径，V_h 是过孔直径。

由式(4)和(5)可得出两相连过孔的角度：

\theta \geq \sin^{-1}\left[\frac{3 \times (V_p - V_h)}{a}\right] \tag{6}

因此 PCB 罗氏线圈的最大匝数：

N \leq \frac{360}{\theta} = \frac{360}{\sin^{-1}\left[\frac{3 \times (V_p - V_h)}{a}\right]} \tag{7}

一般而言，板子厚度也决定了最小过孔的尺寸，因此在设计线圈前，最好与 PCB 制作厂商确认。

1.3.2 合理利用空间

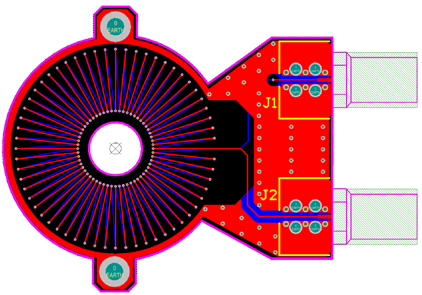
PCB 罗氏线圈一般呈发散式布线，这样在靠近外圈的线匝间将有较大的空隙。因此可以在大线匝之间增加小线匝，这样在板子尺寸不变的情况下，可以增大线圈的互感系数，如 Figure 4 所示。设小线匝的内径为 c，外径为 d，则线圈的互感系数：

M = M_1 + M_2 = N \times \frac{\mu \times h}{2\pi} \times \left(\ln \frac{b}{a} + \ln \frac{d}{c}\right) = N \times \frac{\mu \times h}{2\pi} \times \ln \frac{bd}{ac} \tag{8}

Figure 4 增加小线匝后的罗氏线圈

在板子尺寸固定的情况下，若需要非常大的互感系数，可以考虑将多个 PCB 罗氏线圈进行首尾串联，即以 Figure 4 的 J2 输出连接到下一个 PCB 线圈的 J1，实现信号的叠加。

2 积分电路设计

2.1 理想积分电路的不足及改进

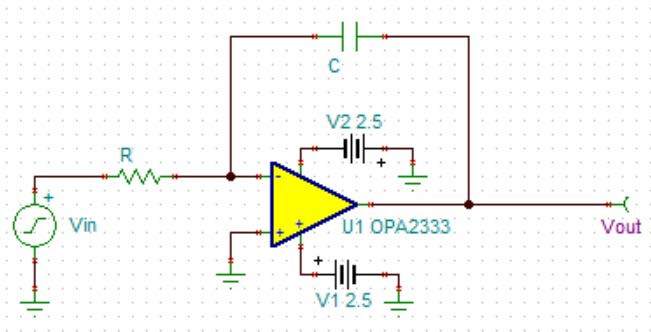
由于罗氏线圈的输出电压是测量电流信号的微分，假若后级没有积分电路，那么只要电流有轻微的高频分量，就会在线圈输出端感应出较高的电压，从而淹没基波信号。因此后级需要积分电路对信号进行还原。理想积分电路如 Figure 5 所示。

Figure 5 左图为理想积分电路的原理图，右图为积分输出电压波形

在输入信号的偏置为零时，积分输出后的波形偏置也应该为零。然而由上图可见，积分输出电压的偏置并不为零，并且波形漂移到了电源轨。实际运放工作的时候情况更糟，波形将会在电源轨上产生削波，造成饱和失真或截止失真。其主要原因是目前的运放都不是理想运放，它存在着固有的失调电压 offset。由于没有其他回路，offset 就会对积分电容进行充电，长时间情况下必然导致电容饱和，导致削波。因此需要在积分电容两端并联电阻，给电容提供放电回路，使电路稳定工作，如 Figure 6 所示。并联电阻后，有必要分析电路的积分性能。

Figure 6 积分电路并联电阻后性能分析

在运放的反相输入端，建立起基尔霍夫电流方程：

\frac{V_{in}}{R} + \frac{V_{out}}{R_f} + C \frac{dV_{out}}{dt} = 0 \tag{9}

式(9)为一阶非线性其次方程，解之得：

V_{out} = C_1 e^{-\frac{t}{R_f C}} - \frac{1}{RC} e^{-\frac{t}{R_f C}} \int V_{in} \times e^{\frac{t}{R_f C}} dt \tag{10}

其中 C_1 为常数。假定输入信号 V_{in} = \cos(\omega t) ，则式(10)可化简为：

V_{out} = C_1 e^{-\frac{t}{R_f C}} - \frac{1}{\omega RC} \sin(\omega t + \varphi),\quad \varphi = \arctan\left(\frac{1}{\omega R_f C}\right) \tag{11}

从频域角度，并联电阻后电路的放大倍数：

A = \left| \frac{V_{out}}{V_{in}} \right| = \left| \frac{R_f \parallel \frac{1}{j\omega C}}{R} \right| = \frac{R_f}{R \sqrt{1 + \omega^2 R_f^2 C^2}} \tag{12}

式(11)和(12)传递了两个重要的信息：

1. 当时间 t 逐渐变大时，输出端电压 V_{out} 的指数部分 C_1 e^{-\frac{t}{R_f C}} 将逐渐变小，最终完全可以忽略不计；
2. 当 R_f \gg \frac{1}{\omega C} 时， \varphi \approx 0^\circ ，且放大倍数接近于理想的 \frac{1}{\omega RC} ，此时可认为输出端电压即为输入信号的反相积分。

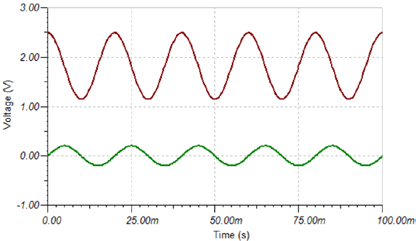
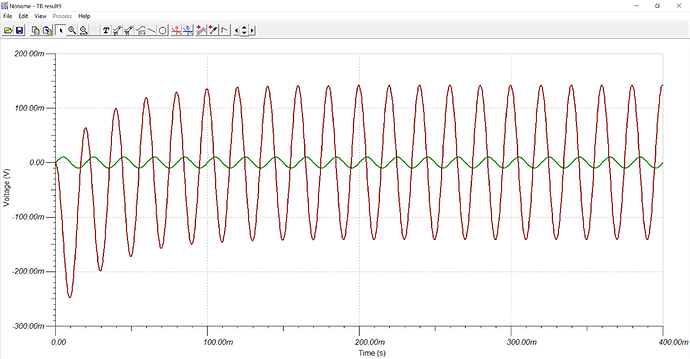
根据以上分析，积分电路仿真结果如 Figure 7 所示。其中绿色曲线为输入，红色曲线为输出。输出信号在初始阶段受指数因子影响而出现了波动，但最终稳定下来，积分效果很好。

Figure 7 并联电阻后积分电路仿真波形

2.2 积分电路运放选型

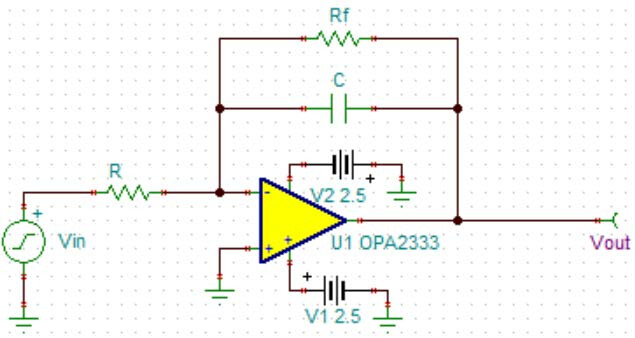
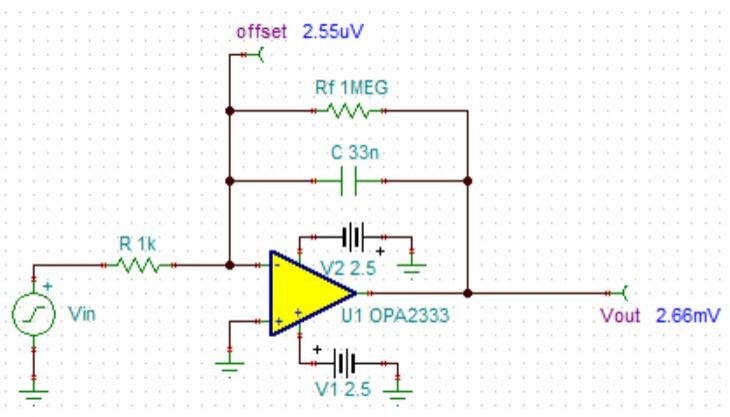
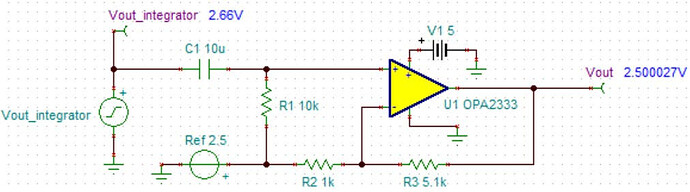
为了达到较好的积分效果，一般需要将反馈电阻 Rf选得尽可能大，但并不是越大越好。其主要原因是积分电路对运放 offset 而言是一个同相放大电路，反馈电阻 Rf过大将导致输出端存在很大的直流偏置，削弱了积分漂移的抑制能力。因此积分电路内的运放应具有非常小的 offset 值，以保证输出端的直流电平尽可能低。OPAx333 是 TI 推出的一款具有 Zero Drift 功能的低 offset 运放，内部采用数字校准的方法大幅降低了 offset 和漂移电压，其 offset 最大值仅为 10uV，同时具有低至 0.05uV/°C 的漂移，非常适合用于积分电路的设计。Figure 8 进行了 OPA2333 积分电路的直流仿真，可以看到在反馈电阻是积分电阻 1000 倍的情况下，输出也仅有 2.66mV，性能非常优良。同时 OPAx333 的最大静态电流仅为 25uA，是一款低功耗高性能运算放大器。

Figure 8 OPA2333 积分电路直流仿真

2.3 单电源积分电路设计

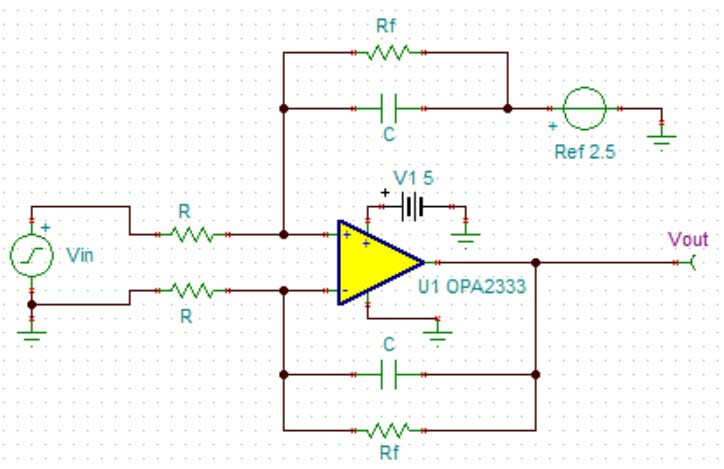
前述积分电路采用的是双电源积分方案，然而不少客户的应用场合只支持单电源供电，因此有必要设计一类单电源积分电路。参考差分运放的电路结构，设计单电源积分电路如 Figure 9 所示。

Figure 9 单电源积分电路

与前述的分析方法类似，假若输入电压 V_{in} = \cos(\omega t) ，则输出电压：

V_{out} = V_{ref} + C_1 e^{-\frac{t}{R_f C}} + \frac{1}{\omega RC} \sin(\omega t + \varphi),\quad \varphi = \arctan\left(\frac{1}{\omega R_f C}\right) \tag{13}

对式(13)的核心解读：

1. 输出特性：输出电压是输入信号的同相积分，同时包含直流偏置 V_{ref} ；
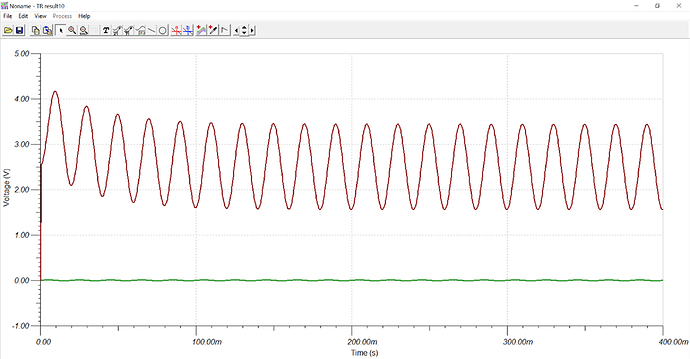
2. 仿真验证：仿真输出波形对应Figure 10，其中绿色曲线为输入信号、红色曲线为输出信号，系统的积分性能表现良好。

Figure 10 单电源积分电路仿真波形

2.4 高性能积分电路注意事项

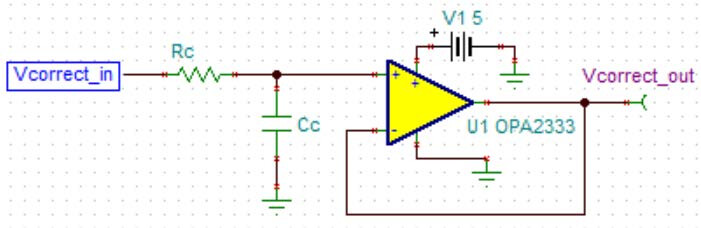
2.4.1 偏置校正

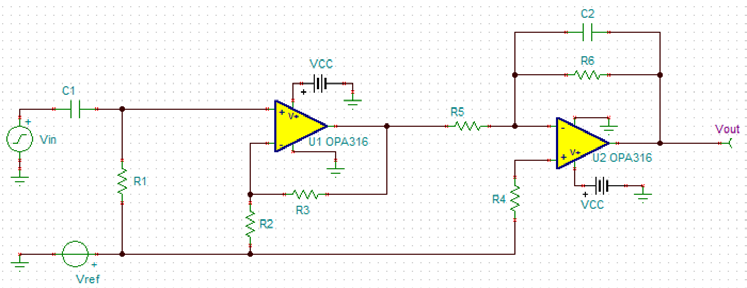
由前述电路分析知，输出端的电压偏置存在一定误差，对 OPAx333 运放而言最多只有几个mV(较差的运放则可能达到数百 mV)。若对输出端的偏置要求较高，则需要重新对偏置进行校正，校正电路位于积分电路的后级，如 Figure 11 所示。由仿真结果可知，输出端 Vout 的直流偏置与预设的 Ref 值之间仅差 27uV, 偏置效果非常优秀。同时同相比例电阻 R2 和 R3 可以对信号进一步地调理，使输出达到满幅。

Figure 11 偏置校正电路及 DC 仿真结果

2.4.2 高频故障分量的测量

在某些应用场合(如 AFCI)，用户主要关注的是电流的高频故障分量，以便在故障情况下做出相应的动作(如切断电路)，这时低频段的正常工作电流便显得不那么重要，甚至可以忽略不计。针对这种应用情况，可以先设置一个高通滤波器，以滤除低频成分。再添加一个放大电路，使高频成分的信号放大，保证积分后的信号足以被监测到，应用电路如 Figure.12 所示。

Figure 12 高频故障分量测量电路

2.4.3 低频相位校正

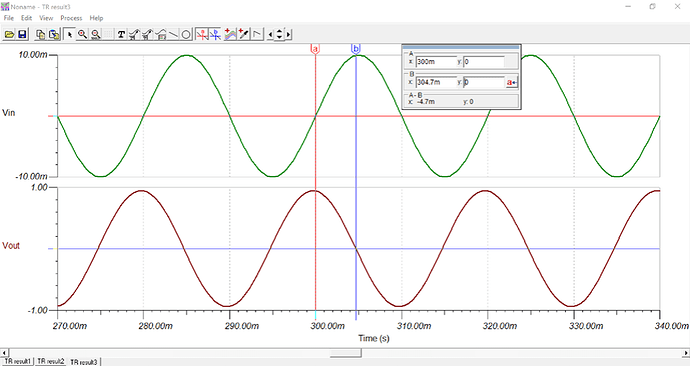
根据前述分析，积分电路存在一定的相角误差，频率越低，相角误差越大。以 Figure 8 中电路为例，在 50Hz 的工作频率下，仿真波形结果如 Figure 13 所示。其中绿色曲线为输入，红色曲线为积分输出。

Figure 13 反相积分电路仿真波形相位分析

理论上，对 50Hz 的正弦信号进行反相积分，积分后的波形过零点应滞后于输入信号 90°，在时域上表现出来的效果就是 b 点滞后 a 点 5ms。然而由 Figure 13 可知，a 和 b 两点间的时间差是 4.7ms，转换成相角后约为 84.6°。也就是说，积分输出波形超前了预期设计约 5.4°相角。一般在两种场合下需要重点考虑相位的校正问题。一是系统对相位的要求较高，如控制断路器的开合，相位不准则产生较大电弧，威胁设备和人身安全；二是系统本身的工作频率较低，如对电力企业而言，工频(50/60 Hz)是主要应用场合，低频带来较大的相角误差。

下面分析相角误差产生机理及校正措施。积分电路的相角误差：

\varphi_1 = \arctan\left(\frac{1}{\omega R_f C}\right) \tag{14}

假若采用了偏置校正电路，也会产生另一个相角误差：

\varphi_2 = \arctan\left(\frac{1}{\omega R_1 C_1}\right) \tag{15}

\varphi_1 和 \varphi_2 均产生了超前相角，因此需要一个滞后校正环节来抵消，如 Figure 14 所示。相位校正主要分有源和无源两类。有源校正效果最好，不受负载阻抗的影响，但是需要额外添加一颗运放，成本较高；无源校正成本非常低，但是校正的效果受负载阻抗的影响，一般视应用需求决定采用哪类方案。为了保证较好的校正效果，积分电路和低频校正电路的电容尽量选用 C0G 或 NP0 系列。

Figure 14 左图为有源相位校正，右图为无源相位校正

3 系统测试

3.1 性能测试

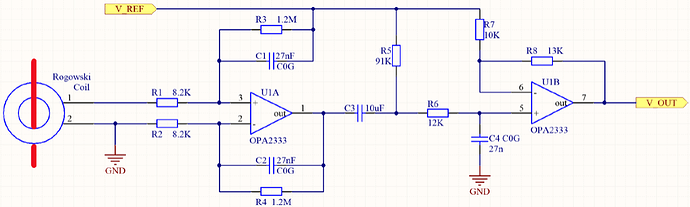
以工频 50Hz 应用场合为例，设计单电源积分电路如 Figure 15 所示。预期设计目标为输出端电压与输入电流呈线性变化，比例系数为 52.4。其中罗氏线圈设计参数为 101nH。

Figure 15 工频应用场合的单电源积分电路原理图

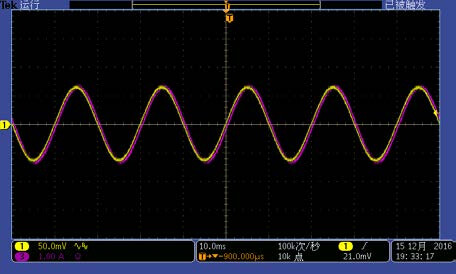
将电流导线垂直穿过 PCB 罗氏线圈，受限于测量设备输出电流较小，故增加了匝数，测量环境及波形如 Figure16 所示。

Figure 16 左图为测量环境，右图为测量波形(紫色部分为电流，黄色部分为积分输出电压)

由 Figure16 右图可知，输出端电压的波形与电流波形基本吻合，达到了较好的测量效果。测量数据整理如 Table1 所示。

Table 1 PCB罗氏线圈测量数据

输入电流(RMS)/A	输出电压(RMS)/mV	输入电流(RMS)/A	输出电压(RMS)/mV
0.46	20.95	2.74	124.8
0.92	42.03	3.26	148.0
1.39	63.02	3.68	166.8
1.83	83.70	4.01	185.4
2.30	104.6	4.46	202.5

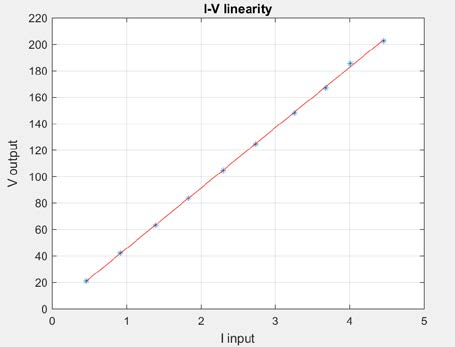
对 Table1 数据进行线性拟合，如 Figure17 所示。结果表明输出电压与输入电流的线性度非常好，近似满足如下关系式：

V_{out} = 45.64 \times I \tag{16}

Figure 17 输出电压与输入电流的线性拟合

根据理论计算，输出电压与输入电流的关系式为：

V_{out} = (N \times I \times \omega \times M) \times \frac{G}{\omega RC} = 47.21 \times I \tag{17}

系数测量结果 45.64 比理论结果 47.21 略小，但误差控制在 5%以内，基本符合预期设计目标。

3.2 性能测试误差分析与改进

测试误差主要由载流导线和线圈的相对位置有关，为了减小误差，一般要求较长的载流导线垂直穿过罗氏线圈的圆心，并尽可能减小线的弯折。本次测试限制于测量电流较小，因此采用了增大匝数的办法提高线圈等效互感系数，故载流导线不全部穿过线圈圆心，且存在较大的线缆弯折，故实测线圈互感系数比理论值小，但差别不大，与设计目标基本吻合。

3.3 干扰测试

罗氏线圈测量电流时，要求被测电流从线圈的中心通孔穿过。然而在实际工作环境中，被测电流周围一般还有其它交变电流（如三相交流电传输场合）。根据罗氏线圈的工作原理，外围交变电流也可以在线圈中产生交变磁场，干扰着被测电流。因此分析罗氏线圈对周围电流的抗干扰能力就显得有必要了。

干扰测试的基本过程是先在无干扰电流情况下，测量输出电压与被测电流之间的对应关系。然后在被测电流周围（即线圈外）添加干扰电流，检验在同一被测电流下的积分输出电压是否改变。根据这种设想，罗氏线圈干扰测试的测量环境如 Figure18 所示。

Figure 18 左图为无干扰电流测量环境，右图为有干扰电流测量环境

受限于测量现场无法提供较大的干扰电流，为了达到更好的干扰效果，被测电流不增加匝数，并使干扰电流与被测电流的大小相当。作为匝数的补偿，在干扰测试中增大了积分电路的放大倍数（Figure15 中的 R7 改成 100Ω）。需要说明的是，放大倍数过大会带来一些弊端，如输出端的 offset 变大，以及放大倍数的实际增益与设计值的偏差增大等。故在实际应用环节不宜选用较大的放大倍数。但在此抗干扰测试中，我们更关注的是在电路固定的情况下，干扰信号对被测信号的影响，因此较大增益带来的影响不大。

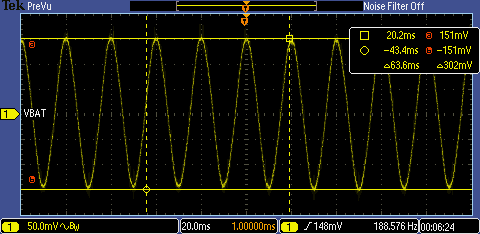
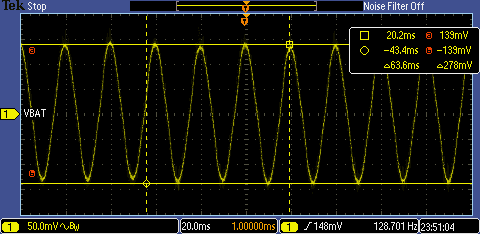
在有无干扰电流情况下，测量到的积分输出电压波形如 Figure19 所示。

Figure 19 左图为无干扰电流下的输出电压波形，右图为有干扰电流下的输出电压波形

进一步将测试数据整理如 Table2 所示。

Table 2 干扰测试数据

被测电流(RMS)/A	干扰电流(RMS)/A	无干扰电流时输出电压(RMS)/mV	无干扰电流时输出电压(RMS)/mV	误差%
0.41	0.41	21.9	20.6	-5.9%
0.82	0.81	43.1	38.9	-9.7%
1.23	1.22	65.1	58.5	-10.1%
1.64	1.63	83.4	78.5	-5.9%
2.06	2.04	106.1	98.3	-7.4%

从 Table2 中可知，干扰电流的引入削弱了输出电压的幅值，导致了测量误差。在本次测试中，误差在 10%左右。

3.4 干扰测试误差分析与改进

当罗氏线圈外存在干扰电流时，由于干扰电流的变化从而产生了交变磁场，交变磁场在罗氏线圈中产生了感应电势，这便是存在测量误差的根本原因。测量误差的大小与干扰电流值有关，也和干扰电流与被测电流的距离有关。在本次测试中，干扰信号非常大，与被测信号大小相当，并且干扰信号与罗氏线圈的距离较短，因此造成了较大的测量误差。在实际测量时应注意将干扰电流远离罗氏线圈，在条件允许的情况下减小干扰电流，便可以减小测量误差。

4 参考文献

1. TI-Design-01063, High Accuracy AC Current Measurement Reference Design Using PCB Rogowski Coil Sensor, Texas Instruments Inc.
2. OPA2333 datasheet 2016, Texas Instruments Inc.